Math for Motorcycles #5 — Gearing and Thrust (or Acceleration)

If you’re like most riders, then you’ve experienced motorcycles with a wide range of power and torque. Your average dirt bike makes a tiny amount of torque, and your average big Harley makes an imperial ton of it.

Your average learner bike (outside the US, because in America, nobody is a learner!) makes a small amount of power, whereas the sexy sport bike you can’t take your eyes off at the dealership makes bucketloads.

But what doesn’t quite add up is that all of these small bikes, despite their apparent disadvantages, can be wheelied, have no problem launching at traffic lights, and give you enough “pull back” on your handlebars to give you the jollies.

Why is this? The answer, as you know, is in gearing. But what’s super interesting to me is how gearing translates to thrust.

What is “Thrust”?

Thrust is literally, in physics terms, acceleration. But I think “thrust” conveys the feeling more viscerally.

As motorcyclists, we understand thrust as the force that pushes us back in our seat and makes us pull on the handlebars in a fight to stay on the bike.

What’s important is that thrust is not “torque”. This is in some ways obvious. But I want to point it out because people often talk about “changing the gearing for more torque”. I know what people are getting at, and I’m really not into semantics. So, the point of this isn’t to correct people. It’s more to help understand how changing one thing changes another.

When you change the gearing of a motorcycle, the engine obviously stays the same. So the engine is producing the same amount of torque, measured in Nm or lb-ft.

Torque is given that metric — a force multiplied by a distance — because that’s what it is! It’s a force measured at the end of a lever, and it describes the twisting force at the center of a lever (or wheel).

The longer the lever or the larger the wheel, the less force at the end. So if you increase the circumference of your rear wheel by 10%, for example, you’ll have 10% less acceleration.

Torque is a component of acceleration or thrust. But two bikes with different gearing and/or weight that have the same torque at the engine perform differently, which is why you need a bit of math to work out how quickly the bike actually accelerates.

For example, a Yamaha YZF-R7 and Ténéré 700 are two bikes that have the same engine but different gearing and wheels. So they accelerate differently.

Model	YZF-R7	XTZ690
Item
Final drive sprocket ratio	16:42 (1:2.625)	15:46 (1:3.067)
Rear wheel size / Diameter	180/55-17 1.98 m	15070-18 2.10m
1st gear thrust (g-force)	1.04 g	1.03
Top speed 1st gear	99 km/h / mph	90 km/h / mph
Top speed 6th gear (i.e. what it’s geared for)	292 km/h / mph	265 km/h
Cruising RPM, 110 km/h (68 mph)	4500 rpm	5000 rpm

To give you a different understanding of thrust, consider fighter planes or rockets destined for space. If you like that stuff, then you know about g-forces.

Space craft and fighter planes are where g-forces are most extreme, distorting people’s faces and making them black out. You might recall the g-forces on Homer Simpson’s Face in the iconic episode Deep Space Homer, which contorted his face first into Richard Nixon’s, then into Popeye’s.

We don’t get close to those G forces on motorcycles. We max out at usually around 1 for mere mortals, or 2 in the case of talented riders using their bikes to the max on slicks in good conditions.

One unit of g-force is equal to one unit of gravitational pull. In mathematical terms, this is 9.8 metres per second per second (9.8 ms^-2), which means “every second, speed increases by 9.8 meters per second (or about 35 km/h or 22 mph)”.

G force is described as acceleration, because if that force (e.g. gravity) were left unchecked, it’d make you accelerate faster and faster until you reached terminal velocity.

Because when we’re standing on the ground we have ground underneath us, if everything is as it should be, then we don’t accelerate. But if you jump out of a plane, then after 1 second, you’ll be going 9.8 meters per second, then after 2 seconds double that, and so on until wind resistance pushes you back enough the other way and you reach that’s your terminal velocity.

Mathematical Definition of Thrust

Technically, thrust is just acceleration, which is defined by force and mass.

F = ma
i.e. Force = mass x acceleration
i.e. Acceleration (thrust) = Force / mass

So more force = more thrust. More mass = less thrust.

The engine makes force. Specifically, the pistons have a downward force onto the crankshaft. That is when force becomes torque — an up-and-down motion becomes a turning one.

When we talk about the torque produced at the crank, that’s what we mean — the rotational force (torque) at the crankshaft.

Here’s the relationship between all the bits of the math that makes up acceleration.

• Torque is the rotational force produced by the motorcycle’s engine. It is measured in Newton-meters (Nm) or pounds-feet (lb-ft) (also known as foot-pounds).
• Force is the final force against the ground after the gearing effect of the drivetrain — the primary drive, the gear ratios, the final drive, and the diameter of the wheel and tire.
• Acceleration is the effect of the force on the weight of the motorcycle. It’s measured in the change in velocity of the motorcycle over time, in meters per second squared (m/s²) or feet per second squared (ft/s²). (This is despite the fact that velocity is conventionally understood as km/h or mph).
• A g-force is a unit of acceleration equal to the force of gravity (9.81 m/s²). We use g-force to express the force exerted on an object, such as a motorcycle or its rider, due to acceleration.

The relationship between these concepts can be summarized as follows:

The engine takes the piston’s force, rotates the crankshaft, and produces torque. This torque is multiplied through the vehicles drivetrain via the primary gear, the gear box, the front and rear gearing (whether via chain, shaft, or belt), and finally via the wheel.

One it hits the ground via the tire’s contact patch, torque finally becomes a linear force. The force pushes backwards on the ground, propelling the motorcycle forwards.

The acceleration of the motorcycle depends on the force and the weight of the motorcycle. The formula is acceleration = force / mass, as mentioned above.

The acceleration in g-force is just that acceleration divided by 9.8 (which is the acceleration rate of gravity). This is what I refer to as “thrust”.

Understanding What Maximum Thrust “Feels” Like

What thrust feels like to you is subjective.

Generally, as I mentioned, thrust feels like a strong, continuous push. It means you’re pushed back in your seat, and that you have a pull-back feeling on the handlebars.

Thrust / acceleration actually has a direction component. In physics, we call it a vector (which is a scalar + a dimension). So you can feel acceleration when accelerating as well as braking — braking is “accelerating in the opposite direction”. (And turning is accelerating to the left or right, but that’s for another day!)

In a physics lab environment, where everything’s in a vacuum and there’s no drag of any kind, when you’re going a constant velocity — whether very fast, or at a standstill — there’s no feeling of “acceleration”. It’s only when you’re going faster, going slower, or turning.

The feeling of thrust depends a bit on the motorcycle you’re on. If you’re on a sport bike and you’re hunched over, then acceleration pushes you a bit back into the seat. If you’re upright, you might get that feeling that you have to hang on to the handlebars for dear life. That’s how people commonly describe riding a power cruiser, for example.

You also feel g-forces in the opposite direction when braking. Again, on a sport bike, this might be the feeling you need to scoot back in your seat to keep the rear wheel on the ground. And on a more standard bike or cruiser, it’ll be pushing against the handlebars or even the forward pegs.

In everyday riding, we rarely go past about 0.75 gs for very long — maybe short bursts for higher g-forces. The reason for this is that a whole g of acceleration translates to a 0-100 mph / 0-100 km/h of under 3 seconds. That’s basically a sport bike at full throttle with maximum traction. It’s very hard to get that level of traction in everyday conditions.

And when braking, one g-force means braking from freeway speeds to a standstill in just a few seconds. Imagine you’re at freeway speeds, then count it down to imagine it: Zero, one, two, three, standstill. That’s a lot of g-force! To do that you’d need good road conditions, good tires, and very steady hands on the brakes — or some kind of braking ride aid.

The thing that stops us from accelerating or braking at much more than 0.75 gs is tire traction. If you accelerate or brake too hard, you break traction. This means burnouts, skids, or just crashes. Not all so bueno (unless you’re trying).

Street tires give way somewhere between 1 -1.5 Gs of acceleration. Once a tire breaks traction, it’s hard to get it again. This is where things get a little complicated. Essentially, we don’t accelerate or brake linearly. Even if you have the steadiest hand in the world, engines (well, combustion engines) delivery torque in generally a non-linear fashion. Then add into the fact that your squishy, organic hand, managed by your imperfect computer of a brain, rarely will apply throttle or brakes linearly.

The non-linear nature of acceleration or braking means that you might momentarily exceed the limits of traction. So if your hypothetical pattern of braking g-force looks like 0.5, 0.6, omg 1.5, 1.0, 0.2, then the 1.5 is where you’ll brake traction and you’ll never get a chance to do the rest as you’re already skidding.

So if you’re wondering what 1 g-force feels like, generally on a motorcycle it’s this: 1 unit of g-force is about the maximum thrust you can apply without being afraid of losing traction at the rear wheel. Get out there, accelerate as fast as you can without skidding, and that’s it.

How Do You Calculate Thrust?

There are two ways of getting to thrust: from torque or power.

I personally find torque easier to understand mathematically. But I’ll mention power briefly. You can think of power as the amount of energy that an engine pours into a motorcycle.

For example, if a motor makes 100 kW (about 135 hp) of power at 10000 rpm, then it’s making 1000 joules per second of kinetic energy at that moment (or the less easy-to-explain imperial equivalent). That energy gets poured into the motorcycle as “kinetic energy”.

Kinetic energy is the stored energy of a moving thing. It’s a factor of weight and the square of speed. So if something is going twice as fast, it has four times the energy — this is why bullets, which don’t weigh much, can have such destructive potential. And it’s why going a bit faster is more than a bit more dangerous.

Some of that power from the engine is lost in the drivetrain, but let’s ignore that for convenience. This is a physics lab, not reality!

OK, now on to calculating thrust from torque, which is easier.

To calculate the thrust generated by a motorcycle, you follow several steps.

1. Use engine torque and gearing to calculate force.
2. Convert force to acceleration, bearing in mind the weight of the motorcycle (and rider)
3. Convert acceleration to thrust.

1. Calculate torque at the rear wheel

First, figure out what the torque of your motorcycle is. For this, you need to know the rear wheel torque.

You can look at any dyno chart for this. What I like to do is think about the “plateau” of peak torque, not the absolute peak number (which isn’t always the same).

In a road bike, like the Yamaha MT-09, there’s generally a plateau in the middle part of the rpm range. But in a high-power sport bike, like a Yamaha YZR-R1, the plateau of torque is much higher in the rev range. See this chart below I made on the subject, for example.

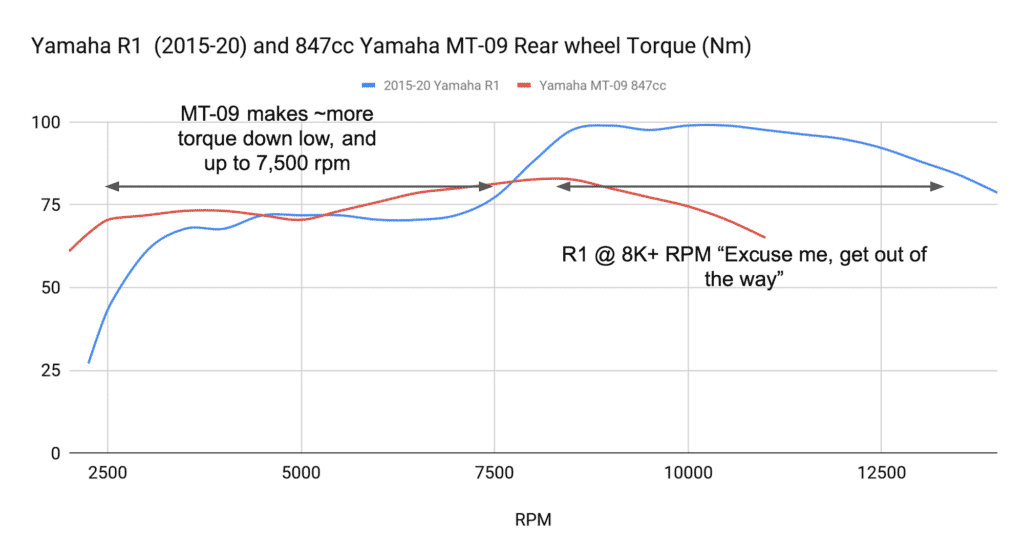
So for the 847 cc Yamaha MT-09, I’d say it makes “around 80 Nm at the rear wheel” between 6000 and 9000 rpm. Bit more sometimes, a bit less, but whatever.

When you read a torque curve from a dyno, you should know that they’re measuring torque on the dyno wheel and then doing math to show you what the dyno at the crankshaft is. So you need to take that number of 80 Nm and multiply it by the various gearing ratios.

You can find the gearing in the motorcycle’s manual near the end.

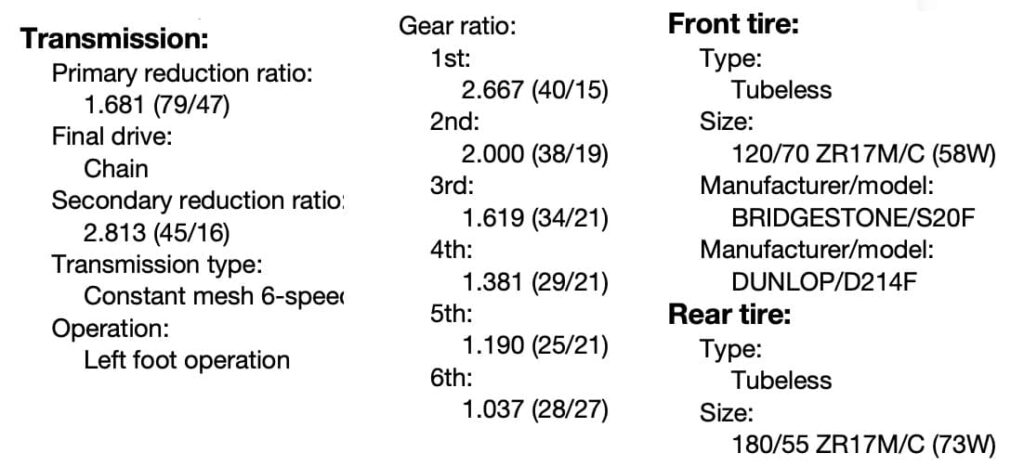
For the above graphic, I combined various sections showing the different gearing ratios (they’re spread over a couple of pages).

So you get 80 Nm and multiply it by 1.681 (the primary drive), 2.667 (the first gear ratio), and 2.813 (the final drive ratio). You get 80 times 12.61 or 1008 Nm — that’s the geared torque at the rear wheel.

The combined final ratio for the gears of an MT-09 is show in in this table:

Gear	Total gearing ratio
1	12.61
2	9.45
3	7.65
4	6.53
5	5.63
6	4.90

Calculate force at the rear tire

Now that you have the torque at the rear wheel, you have to work out the force at the contact patch.

Force pushes the bike forwards.

So take that value of 1008.8 Nm, and divide it by the radius of the tire. A Yamaha MT-09 has a 180/55-17 tire, which means its diameter is 17 inches + 2 x the tire wall, which is 55% of 180 mm. If a tire standard can combine imperial and metric units, then maybe we can all get along! Anyway…

• Diameter = 17 inches + 2 x 55% x 180mm
• = 17 x 25.4 mm + 2 x 99
• = 431.8 + 198
• = 629.8
• So the radius = 629.8 / 2
• = 314.9 mm
• = 0.3149 m

Since the force = 1008.8 Nm, with a radius of 0.3149 m, you get a force of 3204 Newtons on the rear tire.

Calculate acceleration

To calculate acceleration, you use the formula

Acceleration (a) = Force (F) / Mass (m)

The weight of the motorcycle is 189 kg + whatever you weigh + your gear. Let’s assume you weigh 85 kg (185 lb), which is generally a median weight. No judgement if you’re above or below that!

So the total weight of the motorcycle is 189 + 85 = 274 kg.

Acceleration is thus as follows:

• A = 3204 / 274
• = 11.7 m/s^-2

That’s 11.7 meters per second per second, which means that in theory, the Yamaha MT-09 should have a 2.3 second 0-60 mph (60 mph is 26.8 m/s).

This obviously isn’t achievable. The most aggressive claims I’ve seen have been around 2.7 seconds. I’ve seen others around 3.3, which sounds more achievable — and you’d still need to be pretty even-handed and experienced.

The limiting factors are some simplifications we’ve made, plus traction. We’ll get to that later.

Convert acceleration to thrust

With the acceleration value obtained, you can convert it to thrust (or g-force) by dividing the acceleration by the acceleration due to gravity (g = 9.81 m/s²):

• Thrust (g-force) = Acceleration (a) / g
• =11.7 / 9.8
• = 1.19 g

This value represents the amount of thrust experienced by the motorcycle and rider in terms of g-forces.

Unless you have race slicks on and are riding in perfect conditions, it’s pretty unlikely you’ll see that figure. And if you do, you’ll only see it for a second.

Let’s talk about why it’s hard to reach maximum thrust below.

The Limits of Thrust: Torque curves, Tires and Traction

The above is all “in a physics lab” as my all teachers used to say. Let’s come out of the lab and into reality.

In reality, there are a few things that prevent you from getting the extreme g-forces calculated above.

Firstly, the torque curve of any bike is non-linear. Right off idle, there’s nowhere near as much torque as in the “meat” of the torque curve. No matter what bike you’re on — whether a cruiser or a sport bike — if you want to get off the line in a hurry, you have to give it some gas!

Keeping the revs in the meaty part of the torque curve as you launch is one of the challenges of launching quickly. It’s a skill that drag racers spend a long time mastering (among other things).

The above calculation, for example, assumes you’re around 7-8000 rpm of a Yamaha MT-09. It’s quite hard to do that at launch.

The second challenge to getting maximum thrust is tires.

Even though tires are constantly improving, there’s always a limit to just how “sticky” they can be. On a motorcycle this is even harder because the tires are (usually) round, which means the contact patch is quite small. This is one reason why drag bikes use fatter tires.

And finally, traction generally.

Beyond tires, there are a few other elements that dictate how easy it is for your motorcycle to put power to the ground without skidding and doing a burnout. These include how good the suspension is, the motorcycle’s geometry, and weight distribution over the motorcycle.

The Reality Check: Thrust of Various Motorcycles

The reason I wrote this motorcycle is because of an observation I made: Even very average cars have no problem jumping off the line and getting to low-speed city speeds.

Same with motorcycles. You don’t NEED to have a 200 hp sport bike or 150 lb-ft cruiser to get to 40 mph / 60 km/h quickly. So… why is that? Why can vastly different bikes keep up with each other in the early stages?

The answer is the thrust difference from the torque, gearing, and weight.

The result of this can be quite surprising. Middleweight sport bikes (see here for a complete guide) can actually do a decent job of keeping up with 600-750 cc sport bikes (the kind that have 3-4 cylinders and a fairing) up to freeway speeds. After that, the sport bikes take off, of course.

Here’s the peak power and peak calculated thrust in first gear (using the above method) of a few very different motorcycles:

Motorcycle	Brief description	Peak power (rear wheel)	Peak thrust (G force)
BMW R nineT	Retro sport bike, 1170 cc boxer twin, ~220 kg	70 kW / 95 hp @ 7500 rpm	0.96
BMW S 1000 R	Sport naked, 999 cc inline four, ~200 kg	118 kW / 160 hp @ 11000 rpm	1.33
Ducati Monster 937	Sport naked, 937 cc L-twin, ~185 kg	70 kW / 95 hp @ 9600 rpm	1.16
Harley-Davidson Sportster S	Middleweight cruiser, 11xx cc liquid-cooled V-twin	82 kW / 111 hp @ 8400 rpm	1.31
Suzuki SV650	Middleweight sport bike, 645 cc V-twin	50 kW / 68 hp @ 8900 rpm	0.99
Yamaha Bolt	Middleweight cruiser, 942 cc air-cooled V-twin	37 kW / 50 hp @ 5350 rpm	0.89

You can see that the G force is semi random. The Harley-Davidson Sportster S makes a ton of it, probably because Harley-Davidson geared it low so people wouldn’t think it was gutless off the line (the liquid-cooled engine doesn’t respond the way their big air-cooled ones do). And as another random example, the SV650 is pretty spritely despite its low power output — again, because of its gearing.

So if you live your life under 100 mph most of the time (which most people do on the roads), there’s a lot of fun to be had with simpler, cheaper, and often much more comfortable motorcycles.

Wrap up

As you can see, you don’t have to have a massive engine to have big pull-back on the bars. A lot of small engines can do it, too, with the right gearing — though you might run out of headroom more quickly!

If you have a motorcycle with a setup that lets you change the gearing (anything but a shaft), then you can experiment with different sprocket/pulley and chain/belt combinations to opt for different amounts of acceleration or top speed, whatever is your flavour.

Hope this was useful. If you have any comments (or corrections / clarifications), please drop them below.